A standing tower stands on a horizontal plane and is surmounted by a vertical flag staff of height \(h\). At a point on the plane, the angles of elevation of the bottom and the top of the flag staff are \(\alpha\) and \(\beta\), respectively. Prove that the height of the standing tower is \(\left(\frac{h \ tan \ \alpha}{tan \ \beta - tan \ \alpha} \right)\).
Proof:
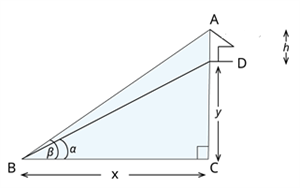
Let \(AD\) denote the height of the flag staff, and \(CD\) denote the standing tower.
Let \(BC\) denote the horizontal plane.
Here, \(AD = h\), \(CD = y\) and \(BC = x\).
In \(\triangle DBC\), we have:
\(x =\) ---- (\(1\))
In \(\triangle ABC\), we have:
\(x =\) ---- (\(2\))
From equations (\(1\)) and (\(2\)), we have:
\(=\)
Simplifying the expression, we get:
\(y =\)
Therefore, the height of the standing tower is \(\left(\frac{h \ tan \ \alpha}{tan \ \beta - tan \ \alpha} \right)\).
Hence, we proved.
Answer variants:
\(\left(\frac{h}{tan \ \beta - tan \ \alpha} \right)\)
\(\left(\frac{h \ tan \ \alpha}{tan \ \beta - tan \ \alpha} \right)\)
\(\frac{h + y}{tan \ \beta}\)
\(\frac{tan \ \beta}{h + y}\)
\(\frac{tan \ \alpha}{y}\)
\(\frac{y}{tan \ \alpha}\)