Akhil is flying a kite with a rope of length 147 \(m\) from a building of height 12 \(m\) above the ground. He observes the kite at an angle of 30\(^{\circ}\). His friend Dinesh observes the kite at an angle of 60\(^{\circ}\) from the ground. If they both are on the opposite sides of the kite, find the distance of the kite from Dinesh. (Use \(\sqrt{3} = 1.732\) and \(\sqrt{2} = 1.414\))
Answer:
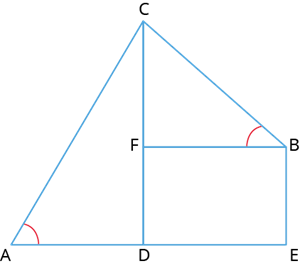
Let \(A\) and \(B\) denote the position of Dinesh and Akhil, respectively.
Let \(AE\) denote the distance between the two friends Akhil and Dinesh.
Let \(AC\) denote the distance of the kite from Dinesh.
Let \(BC\) denote the length of the rope and \(BE\) denote the height of the building.
In the right \(\triangle CFB\), \(sin \ 30^{\circ} =\)
\(CF=\)\(m\)
\(CD = \)\(m\).
In the right \(\triangle CDA\), \(sin \ 60^{\circ} = \)
The distance of the kite from Dinesh is .
(Note: Round off the answer to \(2\) decimal places.)