A girl was flying in a parachute. She observes the top of the mountain at an angle of elevation of 45\(^{\circ}\) and the bottom of the mountain at an angle of depression of 60\(^{\circ}\). If a line is drawn straight beneath the parachute, the distance from the point to the mountain is 875 \(m\), then find the height of the mountain . (Note: Use \(\sqrt{3} = 1.732\))
Answer:
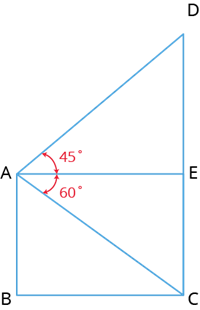
Let \(AB\) denote the altitude of the girl flying in parachute above the ground.
Let \(CD\) denote the height of the mountain, and \(BC\) denotes the distance of the line drawn line straight beneath the parachute to the mountain.
Draw \(AE \perp CD\).
\(DE=\)\(m\).
\(EC=\)\(m\).
Height of the mountain is \(=\) \(m\).