The angle of elevation of a cloud from a point \(c\) metres above the surface of a lake is \(\theta\) and the angle of depression of its reflection in the lake is \(\phi\), then find the height of the cloud above the lake.
Answer:
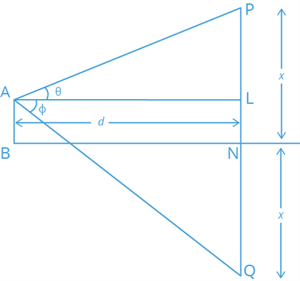
Let \(A\) be the point of observation. Let \(P\) be the cloud, and \(Q\) be the point of its reflection on the lake.
\(tan \ \theta = \)
\(tan \ \phi =\)
The height of the cloud above the lake is