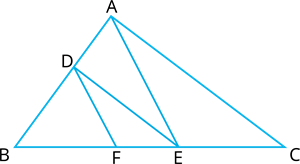
If
\(DE\) is drawn parallel to
\(
AC\) and
\(DF\) is drawn parallel to
\(
AE\) in the figure, prove that
\(\frac{BF}{FE}=\frac{BE}{EC}\).
Proof:
In \(\Delta ABC\),
\(DE ||\)
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
\(\frac{BE}{EC} =\) - - - - (1)
In \(\Delta AEB\),
\(DF ||\)
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
\(\frac{BF}{FE} =\) - - - - (2)
From (1) and (2) we get,
Answer variants:
\(\frac{BD}{DA}\)
\(AC\)
\(\frac{BF}{FE} = \frac{BE}{EC}\)
\(AE\)
\(\frac{BE}{EA}\)