In the provided diagram,
\(A\), \(
B\), and \(
C\) are on the rays \(OP\), \(OQ\) and \(OR\). If \(AB||PQ\) and \(AC||PR\). Examine that \(
BC\) is parallel to \(Q
R\).
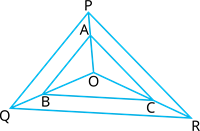
Proof:
We know that, If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
In \(\Delta OPQ\),
\(AB ||\)
\(\frac{OA}{AP} = \) - - - - (1)
And also in \(\Delta OPR\),
\(AC ||\)
\(\frac{OC}{CR} = \) - - - - (2)
From (1) and (2),
\(\frac{OC}{CR} =\)
In \(\Delta OQR\),
\(\frac{OC}{CR} = \frac{OB}{BQ}\)
By theorem,
Thus, \(BC||QR\).
Answer variants:
\(PR\)
\(\frac{OA}{AP}\)
\(PQ\)
\(\frac{OB}{BQ}\)