If in quadrilateral
\(
ABCD\), the diagonals cut each other at
\(O\) such that \(\frac{AO}{BO}=\frac{CO}{DO}\). Determine that
\(
ABCD\) is a trapezium.
Proof:
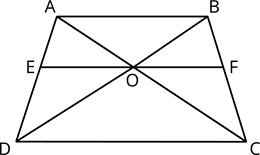
Let us draw a line \(EF||AB\) passing through the point \(O\).
Given \(\frac{AO}{BO} = \frac{CO}{DO}\) - - - - - (1)
Now, in \(\Delta ADB\),
\(EO || \)
By
\(\frac{AE}{DE} = \)..........(i)
But, \(\frac{OA}{OB}=\frac{OC}{OD}\) [given]
\(\Rightarrow \frac{OA}{OC}=\frac{OB}{OD}\)..........(ii)
From (i) and (ii),
\(\frac{AE}{DE} =\)
Thus, in \(\Delta ADC\),
\(\frac{AE}{DE} = \)
Line \(EO\) divides the triangle in the same ratio.
Therefore, \(EO||\).
But, we know that \(EO||AB\)
\(EO||AB||DC\)
Thus, \(AB||\).
Hence, one pair of opposite sides of quadrilateral \(ABCD\) are parallel.
Therefore, \(ABCD\) is a trapezium.