In the given trapezium\(
ABCD\) with parallel sides
\(AB\) and
\(
DC\), the diagonals cross at point
\(
O\). Demonstrate that \(\frac{AO}{BO}=\frac{CO}{DO}\).
Proof:
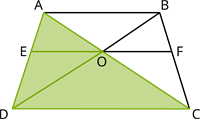
In \(\Delta ADC\),
\(EO||\)
By
So, \(\frac{AE}{DE} =\) - - - - - (1)
Similarly, in \(\Delta DBA\)
\(EO||\)
\(\frac{AE}{DE} =\) - - - - - (2)
From (1) and (2) we proved the result.
Answer variants:
\(\frac{BO}{DO}\)
\(DC\)
\( \frac{AO}{DO}\)
\( \frac{AO}{CO}\)
\(\frac{BO}{CO}\)
\(AB\)