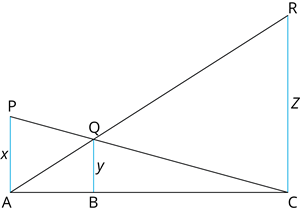
In the given figure \(PA\), \(QB\) and \(RC\) are each perpendicular to \(AC\). If \(AP = x\), \(BQ = y\) and \(CR = z\), then prove that \(\frac{1}{x} + \frac{1}{z} = \frac{1}{y}\).
Proof:
Consider \(\Delta CAP\) and \(\Delta CBQ\)
\(\angle CAP = \angle \) ()
\(\angle PCA = \angle \) ()
Thus, \(\Delta CAP \sim \Delta CBQ\) (by ).
Hence, \(\frac{BQ}{AP} = \).
\(\frac{y}{x} = \frac{BC}{AC}\) - - - - (i)
Consider \(\Delta ACR\) and \(\Delta ABQ\)
\(\angle ACR = \angle \) ()
\(\angle QAB = \angle \) ()
Thus, \(\Delta ACR\) and \(\Delta ABQ\) (by ).
Hence, \(\frac{BQ}{CR} = \frac{AB}{AC}\).
\(\frac{y}{z} = \frac{AB}{AC}\) - - - - (ii)
Add equations (i) and (ii).
\(\frac{y}{x} + \frac{y}{z} = \frac{BC}{AC} + \frac{AB}{AC}\)
\(y \left(\frac{1}{x} + \frac{1}{z}\right) = \frac{BC + AB}{AC}\)
\(y \left(\frac{1}{x} + \frac{1}{z}\right) = \)
\(y \left(\frac{1}{x} + \frac{1}{z}\right) = 1\)
\(\frac{1}{x} + \frac{1}{z} = \frac{1}{y}\)
Hence proved.