Given that
\(AD\) and \(
PM\) are medians of triangles
\(ABC\) and
\(
PQR\) respectively, and \(\Delta ABC\) is similar to \(\Delta PQR\).. Demonstrate that \(\frac{AB}{PQ}=\frac{AD}{PM}\).
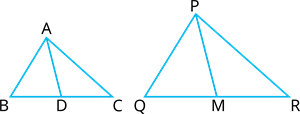
Proof:
Since \(AD\) is the median of \(\Delta ABC\)
\(BD =\) \( = \frac{1}{2}\)
Similarly, \(PM\) is the median \(\Delta PQR\)
\(QM = \) \(= \frac{1}{2}\)
Given \(\Delta ABC \sim \Delta PQR\).
Corresponding sides of similar triangle are proportional.
So, \(\frac{AB}{PQ} = \frac{BC}{QR}\)
\(\frac{AB}{PQ} = \frac{2BD}{2QM}\) (since \(AD\) and \(PM\) are medians)
\(\frac{AB}{PQ} = \frac{BD}{QM}\) - - - - - (1)
Since \(\Delta ABC \sim \Delta PQR\)
Corresponding angles of similar triangles are equal.
\(\angle B = \angle\) - - - - - (2)
Now, in \(\Delta ABD\) and \(\Delta PQM\)
\(\angle B = \angle Q\) (from (2))
\(\frac{AB}{PQ} = \frac{BD}{QM}\) (from (1))
Thus, \(\Delta ABD \sim \Delta PQM\) (by )
Since corresponding sides of similar triangles are proportional.
\(\frac{AB}{PQ} = \frac{AD}{PM}\)
Hence proved.