In \( \triangle ABC \) and \( \triangle PQR \), the sides \( AB \) and \( AC \) and the median \( AD \) are proportional to the sides \( PQ \) and \( PR \) and the median \( PM \), respectively. Confirm that two triangles are similar..
Proof:
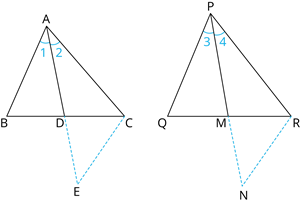
Given, that in triangles \(ABC\) and \(PQR\) in which \(AD\) and \(PM\) are medians such that \(\frac{AB}{PQ} = \frac{AC}{PR} = \frac{AD}{PM}\).
Construction : Produce \(AD\) to \(E\) so that \(AD = DE\). Join \(CE\).
Similarly, produce \(PM\) to \(N\) such that \(PM = MN\). Also, join \(RN\).
In \(\Delta ABD\) and \(\Delta CDE\),
\(AD = \) (by construction)
\(BD = \) ()
\(\angle ADB =\) ()
Thus, \(\Delta ABD \cong \Delta CED\) (by )
\(AB = \) (by ) - - - - (i)
In \(\Delta PQM\) and \(\Delta MNR\),
\(PM = \) (by construction)
\(QM = \) ()
\(\angle PMQ = \) ()
\(\Delta PQM \cong \Delta MNR\) (by )
\(PQ =\) (by CPCT) - - - - (ii)
Now, \(\frac{AB}{PQ} = \frac{AC}{PR} = \frac{AD}{PM}\)
\( = \frac{AC}{PR} = \frac{AD}{PM}\) (from (i) and (ii))
\(\frac{CE}{RN} = \frac{AC}{PR} = \frac{2 AD}{2 PM}\)
\(\frac{CE}{RN} = \frac{AC}{PR} = \frac{AE}{PN}\)
Thus, \(\Delta ACE \sim \Delta PRN\) (by \(SSS\) similarity criterion)
Therefore, \(\angle 2 = \angle 4\).
Similarly, \(\angle 1 = \angle 3\).
\(\angle 1 + \angle 2 = \angle 3 + \angle 4\)
\( = \angle P\) - - - - (iii)
In \(\Delta ABC\) and \(\Delta PQR\), we have
\(\frac{AB}{PQ} = \frac{AC}{PR}\) (Given)
\(\angle A = \angle P\) (from (iii))
Therefore, \(\Delta ABC \sim \Delta PQR\) (by ).