In the figure, \(ABC\) and \(ANP\) are two right triangles, right angled at \(B\) and \(M\) respectively. Demonstrate that:
(i) \(\Delta ABC \sim \Delta ANP\)
(ii) \(\frac{CA}{PA} = \frac{BC}{NP}\)
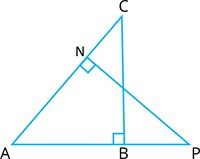
Proof:
(i) Given \(ABC\) and \(ANP\) are two right triangles, \(\angle ABC = 90^\circ\), \(\angle ANP = 90^\circ\)
In \(\Delta ABC\) and \(\Delta ANP\),
\(\angle CAB = \angle\) (Common angle)
\(\angle ABC = \angle\) (Both \(90^\circ\))
Thus, \(\Delta ABC \sim \Delta ANP\) (\(AA\) similarity)
(ii) In the first part we proved, \(\Delta ABC\) and \(\Delta ANP\)
If two triangles are similar, then the ratio of their corresponding sides is proportional.
\(\frac{CA}{PA} = \frac{BC}{NP}\)
Hence proved.
Answer variants:
\(NAP\)
\(ANP\)
\(\frac{CA}{PA} = \frac{BC}{NP} = \frac{AB}{AN}\)