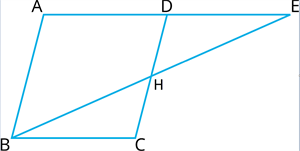
\(E\) is a point on the side \(AD\) produced of a parallelogram \(ABCD\) and \(BE\) intersects \(CD\) at \(H\). Establish that \(\Delta CHB \sim \Delta ABE\).
Proof:
A parallelogram \(ABCD\), where \(E\) is point on side \(AD\) produced and \(BE\) intersects \(CD\) at \(H\).
In parallelogram \(ABCD\), opposite angles are equal.
So, \(\angle A = \angle\) - - - - (1)
Also, in parallelogram \(ABCD\), opposite sides are parallel.
\(AD||BC\)
Since \(AE\) is extended to \(AD\), \(AE||BC\) and \(BE\) is the transversal.
\(\angle AEB = \angle\) (Alternate angles) - - - - (2)
Now, in \(\Delta ABE\) and \(\Delta CHB\),
\(\angle A = \angle\) (From (1))
\(\angle AEB = \angle \) (From (2))
Thus, \(\Delta ABE \sim \Delta CHB\) ( similarity criterion).
Hence proved.