In the below figure, \(\frac{AE}{BE} = \frac{AF}{FC}\) and \(\angle BEF = \angle CFE\), show that \(\Delta ABC\) is an isosceles triangle.
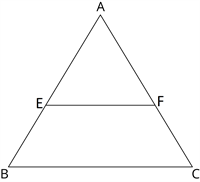
Proof:
Given that \(\frac{AE}{BE} = \frac{AF}{FC}\)
It implies that \(EF ||BC\), by the converse of basic proportionality theorem.
\(\Rightarrow \angle AEF = \angle AFE\) - - - (i)
Now, \(\angle AEF = \angle\) ( angles) - - - (ii)
\(\angle AFE = \angle\) ( angles) - - - (iii)
From eqn (i), (ii) and (iii), we get
\(\angle ABC = \angle\)
Sides opposite to equal angles are equal.
\(\Rightarrow AB = \)
Therefore, \(\Delta ABC\) is an isosceles triangle.
Hence proved.