If a line drawn parallel to one side of triangle intersecting the other two sides in distinct points divides the two sides in the same ratio, then it is parallel to third side. State and establish the converse of the above statement.
Proof:
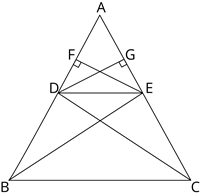
Consider a triangle \(ABC\), \(D\) and \(E\) intersects \(AB\) and \(AC\) respectively.
\(DE\) is parallel to \(BC\).
Join \(BE\) and \(CD\).
Draw \(EF\) and \(DG\) perpendicular to \(AB\) and \(AC\) respectively.

Area of triangle \(= \frac{1}{2} \times bh\)
Area of \(\Delta ADE = \)
Area of \(\Delta BDE = \)
\(\frac{ar \Delta ADE}{ar \Delta BDE}\) \(=\) - - - (i)
Area of \(\Delta ADE =\)
Area of \(\Delta DEC =\)
\(\frac{ar \Delta ADE}{ar \Delta DEC}\) \(=\) - - - (ii)
From the figure, \(\Delta BDE\) and \(\Delta DEC\) lie on the same base \(DE\).
Also, \(\Delta BDE\) and \(\Delta DEC\) lie between the same parallel \(DE\) and \(BC\).
So, area of \(=\) area of
Since the area of the triangles are same, then
Hence proved.
Converse of the theorem:
Statement: If a line divides any two side of a triangle in the same ratio, then the line is parallel to the third side.
Proof:
Draw \(DE'\) parallel to \(BC\) in \(\Delta ABC\).
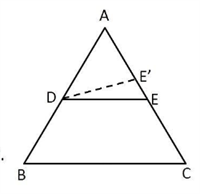

- - - (i)
Given that - - - (ii)
From (i) and (ii), we get
Adding \(1\) on both sides.
\(\frac{AE'}{E'C} + 1 = \frac{AE}{EC} + 1\)
Thus, \(E\) and \(E'\) coincide.
Since .
Hence proved.
Answer variants: