\(D\) is a point on the side \(BC\) of \(\Delta ABC\) such that \(\angle ADC = \angle BAC\). Check that \(BC \cdot CD = AC^2\).
Proof:
Given a triangle \(ABC\) with a point \(D\) on \(BC\) such that \(\angle ADC = \angle BAC\).
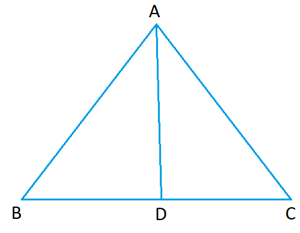
Since \(\angle ADC = \angle\)
By similarity criterion, \(\Delta ADC \sim \Delta\) .
Since they have one and \(\angle ADC = \angle BAC\).
For similar triangles, the ratio of corresponding sides are equal.
\(\frac{AC}{BC} =\)
\(AC^2 = BC \cdot DC\)
Hence proved.