In the given figure, \(\Delta \) \(FEC\)\(\cong \Delta\) \(GDB\) and \(\angle 1 = \angle 2\). Prove that \(\Delta \) \(ADE\)\(\sim \Delta \) \(ABC\).
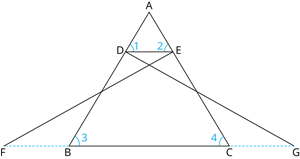
Proof:
Given \(\Delta\) \(FEC\)\( \cong \Delta\) \(GDB\)
Thus, by , \(EC = DB\) - - - - (i)
Also, given that \(\angle 1 = \angle 2\)
\(\implies\) \(AD = AE\)- - - - (ii)
From (i) and (ii), we get
By converse of basic proportionality theorem,
\(DE\)\(||\)\(BC\)
\(\implies\) \(\angle 1 = \angle 3\) and \(\angle 2 = \angle 4\)
In \(\Delta \)\(ADE\) and \(\Delta \)\(ABC\),
\(\angle A = \angle A\) (common)
\(\angle 1 = \angle 3\) (proved above)
\(\angle 2 = \angle 4\) (proved above)
Thus, by similarity criterion \(\Delta \)\(ADE\) \(\sim \Delta\)\(ABC\)