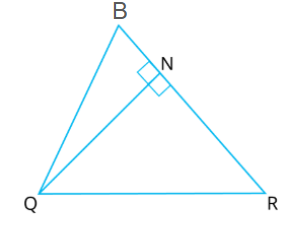
In triangle \(B\)\(QR\), \(N\) is a point on \(B\)\(R\) such that \(QN \perp\)\(B\)\(R\). If \(B\)\(N \cdot NR = QN^2\), show that \(\angle \)\(B\)\(QR = 90^\circ\).
Proof:
In \(\Delta \)\(B\)\(QR\), \(N\) is a point on \(B\)\(R\) such that \(QN \perp \)\(B\)\(R\).
\(B\)\(N \cdot NR = QN^2\)
\(B\)\(N \cdot NR = QN \cdot QN\)
- - - - (1)
If in two triangles, sides of one triangle are proportional to the sides of the other triangle, then their corresponding angles are equal and hence the two triangles are similiar.
So, in \(\Delta QN\)\(B\) and \(\Delta RNQ\),
\(\angle \)\(B\)\(NQ = \angle\) \(RNQ\) (each equal to \(90^\circ\))
Thus, by similarity criterion \(\Delta QN\) \(B\)\(\sim \Delta RNQ\).
We know that , parts of similar triangles are equal.
\(\angle \)\(B\)\(QN = \angle QRN\) and \(\angle RQN = \angle Q\)\(B\)\(N\)
On adding both angles, we get
\(\angle\) \(B\)\(QN + \angle RQN = \angle QRN + \angle Q\)\(B\)\(N\)
\(\angle \)\(B\)\(QR = \angle QRN + \angle Q\)\(B\)\(N\) - - - - (2)
Sum of angles of a triangle \(=\) \(^\circ\)
In \(\Delta \)\(B\)\(QR\),
\(\angle \)\(B\)\(QR + \angle Q\)\(B\)\(R + \angle QR\)\(B\)\( = 180^\circ\)
\(\angle \)\(B\)\(QR + \angle Q\)\(B\)\(N + \angle QRN = 180^\circ\)
\(\angle\) \(B\)\(QR + \angle\)\(B\)\(QR\)\(= 180^\circ\)
\(2 \angle \)\(B\)\(QR = 180^\circ\)
\(\angle \)\(B\)\(QR =\) \(^\circ\)
Hence proved.