In the given figure, \(E\) is a point on side \(CB\) produced of an isosceles triangle \(ABC\) with \(AB = AC\). If \(AD \perp BC\) and \(EF \perp AC\), prove that \(\Delta ABD \sim \Delta ECF\).
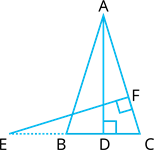
In isosceles triangle \(ACB\),
where \(AB = AC\)
Angles opposite to equal sides are equal.
\(\angle C = \angle\) - - - - (1)
In \(\Delta ABD\) and \(\Delta ECF\),
\(\angle ABD = \angle\) (from (1))
\(\angle ADB = \angle\) (Both \(90^\circ\))
Thus, \(\Delta ABD \sim \Delta ECF\) (by similarity)
Hence proved.