\(O\) is the point of intersection of the diagonals \(AC\) and \(BD\) of a trapezium \(ABCD\) with \(AB||DC\). Through \(O\), a line segment \(PQ\) is drawn parallel to \(AB\) meeting \(AD\) in \(P\) and \(BC\) in \(Q\). Prove that \(PO = QO\).
Proof:
Given \(ABCD\) is a trapezium, the diagonals \(AC\) and \(BD\) intersect at \(O\).
Also, \(PQ||AB||DC\).
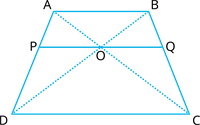
In \(\Delta ABD\) and \(\Delta POD\),
\(PO||AB\) [since \(PQ||AB\)]
\(\angle D = \angle\) (common angle)
\(\angle ABD = \angle\)(corresponding angles)
Thus, \(\Delta ABD \sim \Delta POD\) (by\) similarity criterion).
So, \(\frac{OP}{AB} = \frac{PD}{AD}\) - - - - (i)
In \(\Delta ABC\) and \(\Delta OQC\),
\(OQ||AB\) [since \(PQ||AB\)]
\(\angle C = \angle\) (common angle)
\(\angle BAC = \angle\)(corresponding angles)
Therefore, \(\Delta ABC \sim \Delta OQC\) (by similarity criterion).
So, \(\frac{OQ}{AB} = \frac{QC}{BC}\) - - - - (ii)
Now, in \(\Delta ADC\),
\(OP || DC\)
By basic proportionality theorem,
\(\frac{AP}{PD} = \frac{OA}{OC}\) - - - - (iii)
In \(\Delta ABC\),
\(OQ||AB\) [since \(PQ||AB\)]
By basic proportionality theorem,
\(\frac{BQ}{QC} = \frac{OA}{OC}\) - - - - (iv)
From equations (iii) and (iv),
Adding \(1\) on both sides.
\(\frac{AP}{PD} + 1 = \frac{BQ}{QC} + 1\)
\(\frac{AP + PD}{PD} = \frac{BQ + QC}{QC}\)
\(\frac{AD}{PD}\) =
\(\frac{PD}{AD} = \frac{QC}{BC}\)
\(\frac{OP}{AB} = \frac{OQ}{AB}\) (from equation (i) and (ii))
\(OP = OQ\)
Hence proved.