In the given figure, \(BD\) and \(CE\) intersect each other at the point \(P\). Is \(\Delta PBC \sim \Delta PDE\)? Why?
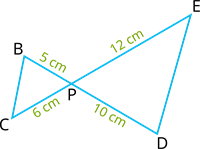
Proof:
In \(\Delta PBC\) and \(\Delta PDE\),
\(\angle BPC = \angle\) (vertically opposite angles)
\(\frac{PB}{PD} =\) - - - - (1)
\(\frac{PC}{PE} =\) - - - - (2)
From equations (1) and (2),
\(\frac{PB}{PD} = \frac{PC}{PE}\)
Since one angle of \(\Delta PBC\) is equal to one angle of \(\Delta PDE\) and the sides including these angles are proportional. So, both triangles are similar.
Thus, \(\Delta PBC \sim \Delta PDE\) (by similarity criterion).
Hence proved.