
Consider a paralleogram shaped window. Draw the bisectors of all its angles. using this construction, prove that the quadrilateral formed by these bisectors is a rectangle.
Proof:
Let \(P, Q, R\) and \(S\) be the points of intersection of the bisectors of \(∠ A\) and \(∠ B, ∠ B\) and \(∠ C\), \(∠ C\) and \(∠ D\), and \(∠ D\) and \(∠A\) respectively of paralleogram shaped window \(ABCD\) as shown in below figure.
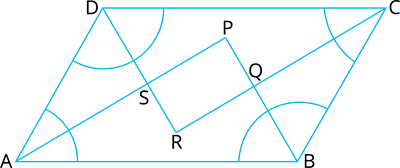
In \(∆ ASD\), \(∠ DAS + ∠ ADS =\) \(=\frac{1}{2} \times \angle A + \frac{1}{2} \times \angle D\)
Since bisects \(∠ D\) and bisects \(∠ A\), therefore,
\(= \frac{1}{2} (∠ A + ∠ D) =\) \(\frac{1}{2}\times\) \(^\circ\)(\(∠ A\) and \(∠ D\) are interior angles on the same side of the transversal)
Therefore, \(∠ DAS + ∠ ADS= \)\(^°\)
Also, \(∠ DAS + ∠ ADS + ∠ DSA = 180^°\) ()
or, \(90^° + ∠ DSA = 180^°\) or,
\(∠ DSA =\) \(^°\)
So, \(∠ PSR =\) \(^°\) ()
Similarly, it can be shown that \(∠ APB = 90^°\)
or \(∠ SPQ = 90^°\) (as it was shown for \(∠DSA\)).
Similarly, \(∠ PQR = 90^°\) and
\(∠ SRQ = 90^°\).
So, \(PQRS\) is a quadrilateral in which all angles are right angles.
We have shown that \(∠ PSR = ∠ PQR =\) \(^°\) and
\(∠ SPQ = ∠ SRQ = \)\(^°\).
So both pairs of opposite angles are equal.
Therefore, \(PQRS\) is a paralleogram shaped window in which one angle (in fact all angles) is \(90^°\) and so, \(PQRS\) is a rectangle.