\(l\) and \(m\) are two parallel lines intersected by another pair of parallel lines \(p\) and \(q\). Show that \(∆ ABC ≅ ∆ CDA\).
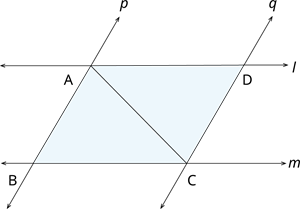
In \(ΔABC\) and \(ΔCDA\), we have:
\(∠ BCA = ∠\) [Alternate interior angles] ---- (1)
\(∠ BAC = ∠\) [Alternate interior angles] ----(2)
\(AC=AC\) [Common side] ---- (3)
Thus, by congruence rule\(ΔABC ≅ ΔCDA\)
Hence, we proved.