\(AD\) and \(BC\) are equal perpendiculars to a line segment \(AB\). Show that \(CD\) bisects \(AB\).
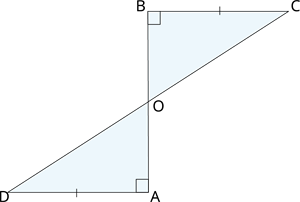
Proof:
In \(ΔAOD\) and \(ΔBOC\), we have:
Here, \(∠ AOD = ∠ \) [Vertically opposite angles] ---- (i)
\(∠ OAD = ∠ \) [perpendiculars] ----- (ii)
\(AD = BC \) [Given] ----- (iii)
Thus, by congruence rule\(ΔAOD ≅ ΔBOC\)
So, \(AO = BO\) [By CPCT]
Hence, \(CD\) bisects \(AB\) at \(O\).
Hence, we proved.