From point
\(D\), lines are drawn parallel to
\(
OQ\) and
\(OR\), meeting the rays at
\(E\) and
\(
F\). Examine that the segment
\(
EF\parallel
QR\).
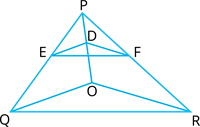
Proof:
In \(\Delta PQO\),
\(DE ||\)
\(\frac{PD}{DO}=\) - - - - (1)
In \(\Delta PRO\),
\(DF ||\)
By
\(\frac{PD}{DO}=\) - - - - (2)
From (1) and (2),
\(\frac{PF}{FR} =\)
In \(\Delta PQR\),
\(\frac{PF}{FR} =\frac{PE}{EQ}\)
By
Thus, \(EF||QR\).
Answer variants:
\(\frac{PF}{FR}\)
\(\frac{PE}{FR}\)
\(OQ\)
\(OR\)
\(\frac{PE}{EQ}\)